【導讀】在實際工程中，應用最為廣泛的調(diào)節(jié)器控制規(guī)律為比例、積分、微分控制，簡稱PID控制，又稱PID調(diào)節(jié)。
在實際工程中，應用最為廣泛的調(diào)節(jié)器控制規(guī)律為比例、積分、微分控制，簡稱PID控制，又稱PID調(diào)節(jié)。
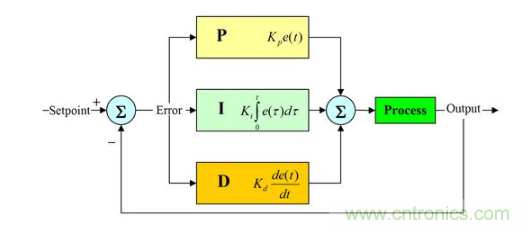
PID控制器問世至今以其結(jié)構(gòu)簡單、穩(wěn)定性好、工作可靠、調(diào)整方便而成為工業(yè)控制的主要技術之一。
當被控對象的結(jié)構(gòu)和參數(shù)不能完全掌握，或得不到精確的數(shù)學模型時，控制理論的其它技術難以采用時，系統(tǒng)控制器的結(jié)構(gòu)和參數(shù)必須依靠經(jīng)驗和現(xiàn)場調(diào)試來確定，這時應用PID控制技術最為方便。即當我們不完全了解一個系統(tǒng)和被控對象，或不能通過有效的測量手段來獲得系統(tǒng)參數(shù)時，最適合用PID控制技術。
PID控制，實際中也有PI和PD控制。PID控制器就是根據(jù)系統(tǒng)的誤差，利用比例、 積分、微分計算出控制量進行控制的。PID控制器的參數(shù)整定是控制系統(tǒng)設計的核心內(nèi)容！
如果你從來沒有接觸過PID，看完這篇文章你就會明白PID控制到底是怎么回事了！
1.假設我們面對的系統(tǒng)是一個簡單的水箱液位，要從空箱開始注水達到某個高度，而你能控制的變量就是注水籠頭的開關大小。這個簡單的數(shù)學模型就是：dx=u。
對于這個系統(tǒng)，我們只需要一個比例環(huán)節(jié)u=k pe就能將其控制住。
此時，kp的大小代表了水龍頭的粗細（即出水量大小對液位誤差的敏感程度，假設水龍頭開度與誤差正比關系），越粗調(diào)的越快，也就是所謂的“增大比例系數(shù)一般會加快系統(tǒng)響應”。如下圖：
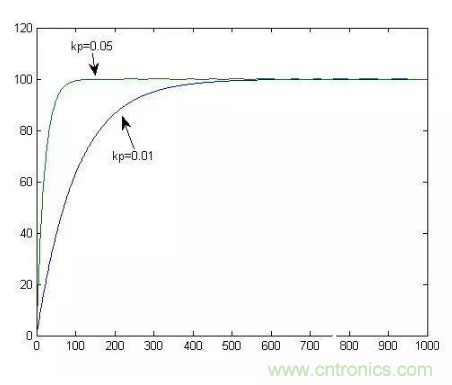
2.假設這個水箱不僅僅是裝水的容器了，還需要持續(xù)穩(wěn)定的給用戶供水。這個系統(tǒng)的數(shù)學模型就需要增加一項：dx=u-c，這里的c是個正的常數(shù)。
我們發(fā)現(xiàn)如果控制器只有一個比例環(huán)節(jié)，那么當系統(tǒng)穩(wěn)定，也就是dx=0的時候，恰好e=c/kp，在系統(tǒng)穩(wěn)定時不為0，液位離我們想要的高度總是差那么一點，這也就是所謂的穩(wěn)態(tài)誤差，或者叫靜差。
這時候c是固定的，那么當然kp越大，e就越小。這也就是所謂的增大比例系數(shù)P在有靜差的情況下有利于減小靜差。如下圖：
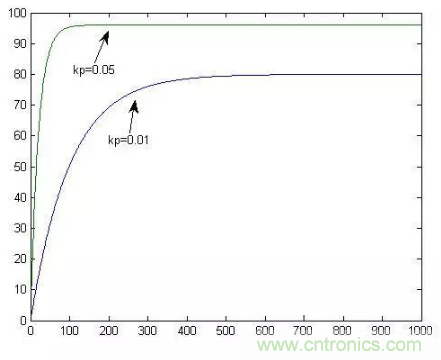
3.從上面的公式e=c/kp可以看出，kp再大也不可能把e變成0。老是調(diào)不到預定位置老板是會罵人的，這可咋辦？
然后有人就想到，第二小節(jié)里頭水箱跟第一小節(jié)的相比，就多了一個漏水的窟窿。它漏多少我給它補多少，那不就成了第一小節(jié)里的簡單系統(tǒng)了么！靠誰補呢？積分環(huán)節(jié)這時候就派上用場了。
我們把之前的控制器變成比例環(huán)節(jié)+積分環(huán)節(jié)：
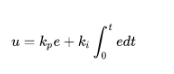
積分環(huán)節(jié)的意義就相當于你增加了一個水龍頭，這個水龍頭的開關規(guī)則是水位比預定高度低就一直往大了擰，比預定高度高就往小了擰。如果漏水速度不變，那么總有一天這個水龍頭出水的速度恰好跟漏水的速度相等了，系統(tǒng)就和第一小節(jié)一樣了。那時，靜差就沒有了。這就是所謂的積分環(huán)節(jié)可以消除系統(tǒng)靜差。
4.什么叫積分時間常數(shù)呢？一般PID控制里，表示積分環(huán)節(jié)敏感度的那個系數(shù)中，Ti就是積分時間常數(shù)。從這個式子我們可以看出，積分時間常數(shù)越大，積分環(huán)節(jié)系數(shù)就越小，積分環(huán)節(jié)就越不敏感（也就是第二個水龍頭越細）。
當只有一個比例環(huán)節(jié)的水龍頭注水的時候，是不會注水注多的，因為離得越近水龍頭關的越小。
但是當用兩個水龍頭注水的時候，在沒到預定高度前第二個積分環(huán)節(jié)的水龍頭可以一直往大了擰，當?shù)竭_預定高度的時候它恰好擰到最大，自然而然就會注水注多了，而多出去的這部分水叫做“超調(diào)”。第二個水龍頭越粗，多注的水就會越多，它調(diào)到恰好等于漏水速度的時間就會越快，同時會多更多波折。
于是，老師告訴我們增大積分時間I有利于減小超調(diào)，減小振蕩，使系統(tǒng)的穩(wěn)定性增加，但是系統(tǒng)靜差消除時間變長。如下圖：
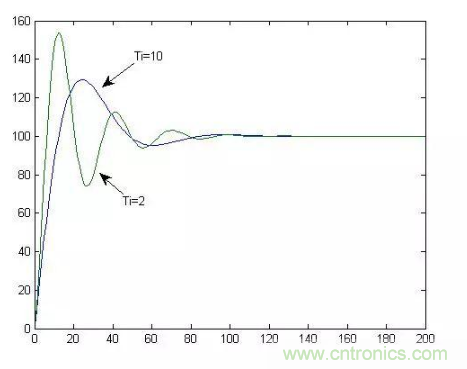
5.接下來看點有意思的東西。還是上面這個系統(tǒng)，假如我們選用相同的積分時間常數(shù)，但是選擇不同的比例系數(shù)會如何呢？
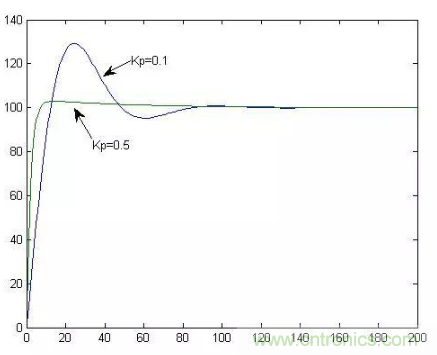
看到上面這幅圖，一些記性好的童鞋可能會有疑問。因為老師明明說過”過大的比例系數(shù)會使系統(tǒng)有比較大的超調(diào)，并產(chǎn)生振蕩，使穩(wěn)定性變壞“，但是上面這幅圖里怎么比例大的反而超調(diào)小呢？
其實上面這幅圖很好解釋，小節(jié)4里我們說明了PI控制器超調(diào)出現(xiàn)原因是積分這個水龍頭在到達目標液位時也恰好開到了最大。而比例這個水龍頭越粗，那么它在超出目標液位時對超調(diào)的抑制也就越明顯。
這里，我想強調(diào)的是： PID參數(shù)整定的結(jié)論是根據(jù)普遍經(jīng)驗總結(jié)的，但是針對某個具體的系統(tǒng)不一定完全適用。
6.在上面的系統(tǒng)中，我們假設用戶用水的固定的一個值，但是實際情況中用戶的用水量往往是變化的。假如我們的系統(tǒng)是dx=u-c（t）呢？
我們試著來分析一下：
我們的控制目標是讓x=xd，系統(tǒng)誤差的定義是：e=xd-x；
那么，誤差狀態(tài)方程就是：；
我們設定的控制目標是個常數(shù)，所以xd=0；
，從這個式子可以看出，當e=0時，不再變化，而c（t）是始終變化的。
此時de不恒為零，也就是說e不恒為零。
當c變成c（t）的時候，e=0就不再是系統(tǒng)的穩(wěn)定平衡點了，經(jīng)典意義上系統(tǒng)不再穩(wěn)定。
7.這里加一個微分環(huán)節(jié)D變成PID控制會不會讓系統(tǒng)重新穩(wěn)定呢？
當加入微分環(huán)節(jié)，
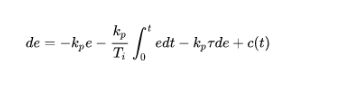
，那么，
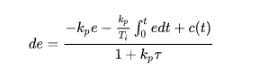
，對于任意，微分環(huán)節(jié)都讓de的變化減慢了。
這也就是“微分環(huán)節(jié)主要作用是在響應過程中抑制偏差向任何方向的變化”，“微分常數(shù)不能過大，否則會使響應過程提前制動，延長調(diào)節(jié)時間”。
至于“微分環(huán)節(jié)會提高系統(tǒng)抗擾動能力，降低系統(tǒng)抗噪聲能力”，更多指的是大多數(shù)細微測量噪聲造成的e很小，但瞬時的de較大，微分環(huán)節(jié)相對于PI環(huán)節(jié)更容易收到這些細微噪聲的影響。
但是，無論如何選取微分參數(shù)，PID控制都不能使系統(tǒng)穩(wěn)定。
從這里，我們可以看到PID控制的局限。
希望大家不要死記口訣，多用所學到的控制理論來針對具體問題具體分析。
免責聲明：本文為轉(zhuǎn)載文章，轉(zhuǎn)載此文目的在于傳遞更多信息，版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問題，請聯(lián)系小編進行處理。
