誤區(qū)一

 

降低電路中的電阻值總是能改善噪聲性能

 

噪聲電壓隨著電阻值提高而增加，二者之間的關系已廣為人知，可以用約翰遜噪聲等式來描述：

 

 

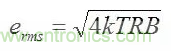
erms為均方根電壓噪聲

 

k為玻爾茲曼常數(shù)

 

T為溫度（單位為K）

 

R為電阻值，B為帶寬

 

這讓許多工程師得出結論：為了降低噪聲，應當降低電阻值。雖然這常常是正確的，但不應就此認定它是普遍真理，因為在有些例子中，較大的電阻反而能夠改善噪聲性能。

 

在大多數(shù)情況下，測量電流的方法是讓它通過一個電阻，然后測量所得到的電壓。根據(jù)歐姆定律V = I ×R，產生的電壓與電阻值成正比，但正如上式所示，電阻的約翰遜噪聲與電阻值的平方根成正比。由于這個關系，電阻值每提高一倍，信噪比可提高3dB。在產生的電壓過大或功耗過高之前，此趨勢一直是正確的。

 

誤區(qū)二

 

所有噪聲源的噪聲頻譜密度可以相加；

 

帶寬可以在最后計算時加以考慮。

 

將多個噪聲源的噪聲頻譜密度加總（電壓噪聲源按平方和開根號），而不分別計算各噪聲源的rms噪聲，可以節(jié)省時間，但這種簡化僅適用于各噪聲源看到的帶寬相同的情況。如果各噪聲源看到的帶寬不同，簡單加總就變成一個可怕的陷阱。

 

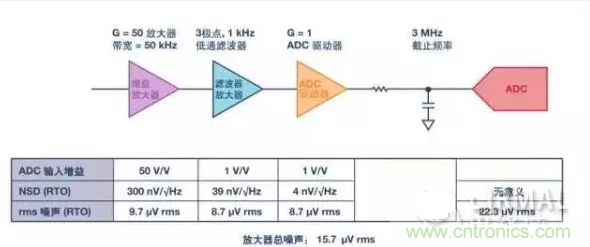
圖1：使用rms噪聲而不是頻譜密度進行噪聲計算的理由

 

圖1顯示了過采樣系統(tǒng)中的情況。從噪聲頻譜密度看，系統(tǒng)總噪聲似乎以增益放大器為主，但一旦考慮帶寬，各級貢獻的rms噪聲其實非常相近。

 

誤區(qū)三

 

手工計算時必須包括每一個噪聲源

 

設計時有人可能忍不住要考慮每一個噪聲源，但設計工程師的時間是寶貴的，這樣做在大型設計中會非常耗時。全面的噪聲計算最好留給仿真軟件去做。

 

不過，設計人員如何簡化設計過程需要的手工噪聲計算呢？答案是忽略低于某一閾值的不重要噪聲源。如果一個噪聲源是主要噪聲源（或任何其他折合到同一點的噪聲源）的 1 / 5 erms 值，其對總噪聲的貢獻將小于2%，可以合理地予以忽略。設計人員常會爭論應當把該閾值選在哪里，但無論是 1 / 3 、 1 / 5 還是 1 / 10 （分別使總噪聲增加5%、2%和0.5%），在設計達到足以進行全面仿真或計算的程度之前，沒必要擔心低于該閾值的較小噪聲源。

 

誤區(qū)四

 

應挑選噪聲為ADC  1 / 10 的ADC驅動器

 

模數(shù)轉換器(ADC)數(shù)據(jù)手冊可能建議利用噪聲為ADC 1 / 10 左右的低噪聲ADC驅動放大器來驅動模擬輸入。但是，這并非總是最佳選擇。在一個系統(tǒng)中，從系統(tǒng)角度權衡ADC驅動器噪聲常常是值得的。

 

首先，如果系統(tǒng)中ADC驅動器之前的噪聲源遠大于ADC驅動器噪聲，那么選擇超低噪聲ADC驅動器不會給系統(tǒng)帶來任何好處。換言之，ADC驅動器應與系統(tǒng)其余部分相稱。

 

其次，即使在只有一個ADC和一個驅動放大器的簡單情況下，權衡噪聲并確定其對系統(tǒng)的影響仍是有利的。通過具體數(shù)值可以更清楚地了解其中的理由。

 

考慮一個系統(tǒng)采用16位ADC，其SNR值相當于100 μV rms噪聲，用作ADC驅動器的放大器具有μV rms噪聲。按和方根加總這些噪聲源，得到總噪聲為100.5 rms，非常接近ADC單獨的噪聲?？梢钥紤]下面兩個讓放大器ADC更為平衡的方案，以及它們對系統(tǒng)性能的影響：

 

如果用似的18位ADC代替16位ADC，前者的額定SNR相當于40 μV rms聲，則總噪聲變?yōu)?1 μV rms。

 

或者，如果保留16位ADC，但更低功耗的放大器代替上述驅動器，該放大器貢獻30 μV rms聲，則噪聲變?yōu)?04 μV rms。

 

就系統(tǒng)性能而言，以上兩種方案之一可能是比原始組合更好的選擇。關鍵是要權衡利弊以及其對系統(tǒng)整體的影響。

 

誤區(qū)五

 

直流耦合電路中必須始終考慮1/f噪聲

 

1/f噪聲對超低頻率電路是一大威脅，然而，許多直流電路的噪聲是以白噪聲源為主，1/f噪聲對總噪聲無貢獻，因而不用計算1/f噪聲。

 

為了弄清這種效應，考慮一個放大器（其1/f噪聲轉折頻率fnc為10 Hz）。對于各種帶寬，計算10秒采集時間內包含和不含1/f噪聲兩種情況下的電路噪聲，以確定不考慮1/f噪聲的影響。其中寬帶噪聲為：

 

 

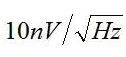
當帶寬為fnc 的100倍時，寬帶噪聲開始占主導地位；

 

當帶寬超過fnc的1000倍時，1/f噪聲微不足道。

 

現(xiàn)代雙極性放大器可以具有比10 Hz低很多的噪聲轉折頻率，零漂移放大器則幾乎完全消除了1/f噪聲。

 

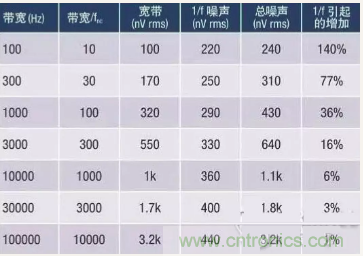
表1：1/f 噪聲影響與電路帶寬的關系示例

 

誤區(qū)六

 

因為1/f噪聲隨著頻率降低而提高，

 

所以直流電路具有無限大噪聲。

 

雖然直流對電路分析是一個有用的概念，但真實情況是，如果認為直流是工作在0 Hz，那么實際上并不存在這樣的事情。隨著頻率越來越低，趨近0 Hz，周期會越來越長，趨近無限大。這意味著存在一個可以觀測的最低頻率，哪怕電路在理論上是直流響應。該最低頻率取決于采集時長或孔徑時間，也就是觀測器件輸出的時長。如果一名工程師開啟器件并觀測輸出100秒，則其能夠觀測到的最低頻率偽像將是0.01 Hz。這還意味著，此時可以觀測到的最低頻率噪聲也是0.01 Hz。

 

現(xiàn)在通過一個數(shù)值例子來展開說明，考慮一個DC至1 kHz連續(xù)監(jiān)控其輸出。如果在前100秒觀測到電路中一定量的1/f噪聲，從0.01 Hz至1 kHz（5個十倍頻程的頻率），則在30年（約1nHz，12個十倍頻程）中觀測到的噪聲量可計算為：

 

 

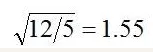
或者說比前100秒觀測到的噪聲多55%。這種增加幾乎沒有任何意義，即使考慮最差情況——1/f噪聲持續(xù)增加到1 nHz（目前尚無測量證據(jù)）——也是如此。

 

理論上，如果沒有明確定義孔時間，1/f噪聲可以計算到一個等于電路壽命倒數(shù)的頻率。實踐中，電路在如此長時間內的偏差以老化效應和長期漂移為而不是1/f噪聲。許多工程師為直流電路的噪聲計算設定0.01 或1 mHz之類的最低頻率，以使計算切合實際。

 

誤區(qū)七

 

噪聲等效帶寬會使噪聲倍增

 

噪聲等效帶寬(NEB)對噪聲計算是一個很有用的簡化。由于截止頻率以上的增益不是0，某些超出電路帶寬的噪聲會進入電路中。NEB是計算的理想磚墻濾波器的截止頻率，它會放入與實際電路相同的噪聲量。NEB大于–3 dB帶寬，已針對常用濾波器類型和階數(shù)進行計算。

 

對于單極點低通濾波器，它是–3dB帶寬的1.57倍，寫成公式就是：

 

 

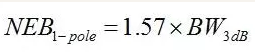
然而，關于應把該乘法因數(shù)放在噪聲公式中的何處，似乎一直存在混淆。請記住，NEB調節(jié)的是帶寬，而非噪聲，因此應在根號下面，如下式所示：

 

 

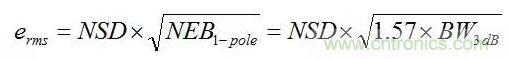
誤區(qū)八

 

電壓噪聲最低的放大器是最佳選擇

 

選擇運算放大器時，電壓噪聲常常是設計人員唯一考慮的噪聲規(guī)格。其實電流噪聲同樣不能忽略。除非在有輸入偏置電流補償?shù)忍厥馇闆r下，電流噪聲通常是輸入偏置電流的散粒噪聲：

 

 

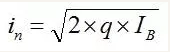
電流噪聲通過源電阻轉換為電壓，因此，如果放大器輸入端前面有一個大電阻，那么電流噪聲對系統(tǒng)噪聲的貢獻可能大于電壓噪聲。電流噪聲會成為問題的典型情況是使用低噪聲運算放大器且其輸入端串聯(lián)一個大電阻時。

 

考慮低噪聲運算放大器ADA4898-1，其輸入端串聯(lián)一個10 kΩ電阻。ADA4898-1的電壓噪聲為：

 

 

10 kΩ電阻的噪聲為：

 

電流噪聲乘以10 kΩ電阻等于：

 

 

這是系統(tǒng)中的最大噪聲源。在類似這種電流噪聲占主導地位的情況下，常?？梢哉业诫娏髟肼曒^低的器件，從而降低系統(tǒng)噪聲；對精密放大器尤其如此，不過高速FET輸入運算放大器對高速電路也可能有幫助。例如，若不選擇ADA4898-1（從而得不到電壓低噪聲的好處），可以選擇AD8033或ADA4817-1等JFET輸入放大器。

 

誤區(qū)九

 

在第一級提供大部分增益可實現(xiàn)最佳噪聲性能

 

為了實現(xiàn)更好的噪聲性能，常常建議在第一級提供增益，這是對的，因為信號會比隨后各級的噪聲要大。然而，這樣做的缺點是會削弱系統(tǒng)能夠支持的最大信號。某些情況下，與其在第一級提供很大一部分增益（雖然這樣可以提高測量靈敏度，但會限制動態(tài)范圍），不如限制第一級提供的增益，并用高分辨率進行數(shù)字化處理，使靈敏度和動態(tài)范圍都達到最大。

 

誤區(qū)十

 

給定阻值時，所有類型電阻的噪聲相同

 

電阻的約翰遜噪聲非常重要，以至于我們需要一個簡單的公式來計算某一電阻在某一溫度下的噪聲。然而，約翰遜噪聲是電阻中可以觀測到的最小噪聲，而且并非所有類型的電阻都有同等噪聲。

 

還有過量噪聲，它是電阻中1/f噪聲的來源之一，與電阻類型密切相關。過量噪聲（有時候也誤稱為電流噪聲）與電流在非連續(xù)介質中流動的方式有關。它被規(guī)定為噪聲指數(shù)(NI)，單位為dB，以每十倍頻程1 μV rms/V dc 為基準。

 

這意味著：如果一個0 dB NI的電阻上有1 V dc 電壓，則給定十倍頻程時的過量噪聲為1 μV rms。碳和厚膜電阻的NI最高，可能高達+10 dB左右，在信號路徑的噪聲敏感部分中最好避免使用。薄膜電阻一般要好得多，約為–20 dB；金屬箔和繞線電阻可以低于–40 dB。

 

誤區(qū)十一

 

給定足夠長的采集時間，

 

均值法可將噪聲降至無限小。

 

一般認為均值法可將噪聲降低均值數(shù)的平方根倍。這在一定條件下是成立的，即NSD必須保持平坦。然而，在1/f范圍內和其他幾種情況下，這種關系不成立。考慮在一個以恒定頻率fs采樣的系統(tǒng)中使用均值法，對n個樣本求均值并進行1/n抽取，返回m個抽取樣本。取n個平均值會將抽取后的有效采樣速率變?yōu)閒s/n，系統(tǒng)看到的有效最大頻率降低n倍，白噪聲降低√n倍。然而，獲得m個樣本的時間也會延長n倍，因此系統(tǒng)可以看到的最低頻率也會降低n倍（記住，沒有0 Hz這種事）。

 

取的均值數(shù)越多，頻段上的這些最大和最小頻率就越往下移。一旦最大和最小頻率均在1/f范圍內，總噪聲便僅取決于這些頻率之比，再提高均值數(shù)對降低噪聲沒有進一步的好處。同樣的道理也適用于多斜率等積分ADC的長積分時間。除了數(shù)學上的限制以外，還存在其他實際限制。

 

若量化噪聲是主要噪聲源，使得直流輸入電壓下的ADC輸出為一個無閃爍的恒定碼，則任何數(shù)量的均值都會返回同一個碼。

 

 

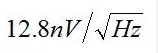
來源：ADI